《原码、反码、补码小程序的设计与实现》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

原码、反码、补码小程序的设计与实现

范文

赵煜马萌

摘要：从机器码出发，介绍了原码、反码、补码的定义以及三者之间的内在联系，由于原码在加减运算中的不足引入了补码，为了方便求得补码又引入了反码，从而清晰地展示了三者编码之间的联系，使用VEE可视化语言实现了三者之间的转化，通过2种方法介绍了负数原码、反码、补码之间的程序设计过程，并且介绍了机器数之间的加减运算方法，以及具体运算过程，使用人工算法验证了该程序设计的正确性。

关键词：原码；反码；补码；运算过程

中图分类号：TP316文献标志码：A文章编号：1008-1739（2020）13-56-4

0引言

计算机能够按照程序自动运算和快速处理大量数据，既可以进行数值计算，又可以进行逻辑计算，还有存储记忆的功能，其中处理的大量数据包括加减乘除运算的数值型数据和不能进行运算的非数值型数据。为了达到方便、容易区分和存储等要求，计算机内部使用二进制存储数据。

计算机中需要原码、补码和反码3种编码，和计算机的硬件有关，二进制的加法，一个异或门就能实现，多位加法器的实现很容易，然而减法没有找到直接的硬件，但是通过补码能把减法转换成加法来做，这样一种硬件执行结构就可以实现加与减2种基本运算。这样就出现了补码，对补码的求解过程，其中一个步骤就刚好形成了反码，反码是原码转换成补码的过渡码。

1原码、反码、补码的基本概念

一个数在计算机中的二进制表示形式叫做这个数的机器数，机器数是带符号的，计算机用机器数的最高位放符号位，正数为0，负数为1。因为第一位是符号位，所以机器数的形式值就不等于真正的数值，将带符号的机器数对应的真正数值称为机器数的真值。原码、反码、补码是机器存储一个具体数字的编码方式，就是为了理解计算机使用二进制进行计算的原理[1]。

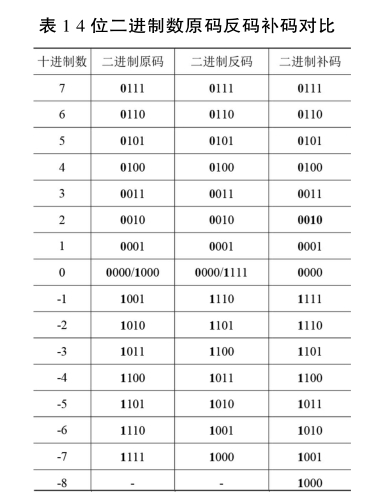
原码是机器数中最简单的一种形式，原码由符号位和数值位两部分构成。数值位部分均保持原来的样子，不需改变。如果是正数，最前面的0视为符号位；如果是负数，最前面的1视为符号位，数值位就是真值的绝对值，原码又称带符号的绝对值。原码进行加减运算时，一个正数和一个负数运算时的结果可能为正也可能为负，而且是绝对值进行比较，这样相对很不方便，因此引入了补码。

反码通常是用来由原码求补码或者由补码求原码的过渡码，反码跟原码是正数时一样；负数时，反码就是原码符号位除外，其他位按位取反。

补码是计算机把减法运算转化为加法运算的关键编码，正数的补码是它本身，负数的补码是除符号位，原码取反加1。

2算法设计过程

2.1 VEE可视化语言

HP VEE是一种主要用于仪器控制和测量处理的可视化编程语言，自1990年以图形化界面和数据流编程为核心的1.0版由HP公司正式发布以来，提升6.0位核心，集成仪器设备控制、高级数据采集以及处理、数据分析等众多先进技术，可用于Windows，SUN，Unix等多种平台的测试软件开发环境。

HP VEE具有以下主要特點：①图形化编程；②丰富的仪器I/O驱动；③虚拟仪器测试；④自动数据类型转化；⑤强大的数学分析能力；⑥开放的编程环境；⑦网络支持。此外，VEE还是一种基于图形式开发、调试和运行程序的集成化环境，其基本编程单元是一系列的图形化功能控件，每个控件都存在一个或多个输入、输出端口，选择合适的端口进行连接，即可完成程序的运行流程。本文主要使用VEE可视化语言实现原码、补码和反码相互转换关系的设计过程，展示原码、补码和反码相互转换关系。

2.2具体实施过程

由于正数的原码、反码、补码都相同，因此正数的转换相对简单，直接符号位为0，真值不变即可。

2.3程序实现原码、反码、补码转换过程

（1）使用定义法实现负数原码、反码、补码之间的转化

原码转化为二进制，取反为反码，再加1为补码。具体使用VEE语言实现程序设计过程为：可选择要转化数的类型，可选择十进制数或二进制数。如果是十进制数需要转换成二进制然后进行求反码和补码。十进制转二进制使用除二法，即div函数和mod函数，被转换数循环执行div/2，并且每个数需要取mod，即除二取余，然后将这些数转化为字符串加起来，即实现了十进制转二进制数。

需要字符串转数组及取反，字符串转数组首先用到strFromLen（str，from，len）函数，输入str为整个字符串，from是从第几个字符开始取，len是要取得的字符长度。其次，字符串转数组要用到Collector函数，该函数实现从strFromLen（str， from，len）函数中取得的单个字符收集起来，组成一个数组，其中Collector函数中Data为单个字符输入，XEQ为输出触发，字符串转数组取反即将0输出为1，1输出为1，即完成了原码转反码的过程。反码转补码需要再加1，此处使用二进制转十进制，然后加1再转为二进制的办法，二进制转十进制使用bits（str）函数，即乘2相加法，上述为使用定义法实现原码、反码、补码之间的转化。

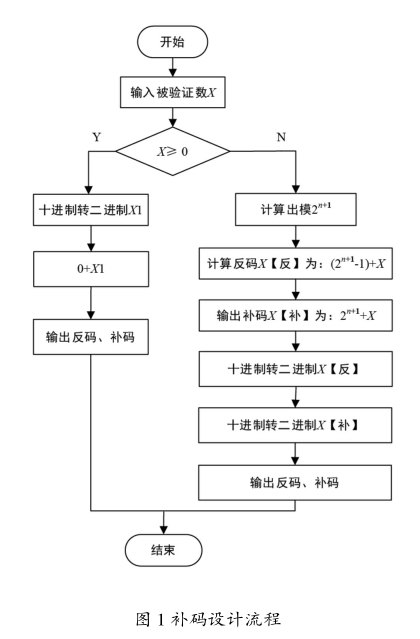
（2）先求模，然后求反码和补码

补码设计流程如图1所示。

2.4补码实现运算过程

CPU中有加法器但没有减法器，通过写出一位全减器的真值表，设计出硬件电路并将其级联，可得到一个减法器，但是大部分情况设计一个减法器还不如用加法器替代，将减数取反加一与被减数相加即可把减法运算转化为加法，将减数取反加一的操作就是将负数用补码的形式表示，也就是用补码这种数值编码方式实现了将减法转变为加法的。

上边已经讲述了补码的计算过程，在进行加减运算时只要将减法转化为加法，然后使用补码计算即可，计算结果再由补码转化为原码即为真实计算结果。

为了便于理解，以钟表来表示，钟表中12点倒退3点就是9点，超过12点重新使用1～12来表示，12是钟表的模，顺时针代表溢出，超过12为溢出，比如10点加5点，为：10+5=15，溢出12，15-12为3点。逆时针为减法，3点往后倒5点从钟表中不难看出是10点，这里减5 h，其实就是计算机中的补码，即12-5，对应7，将减法转化为加法，即3+（12-5）为10点，便于将减法转为加法，“模”的特征为减去一个数等价于加上这个数的补数，计算机引入了模，以负数为例，0> >=-2 ，此时模为2+1。

钟表中，如果9点+8点=17点对应钟表的5点，此处即有一个溢出的概念，在计算机中也存在溢出，溢出即一个位二进制的补码，其表达范围是-2-1+1～2-1-1，如果超出这个范围就称为溢出。

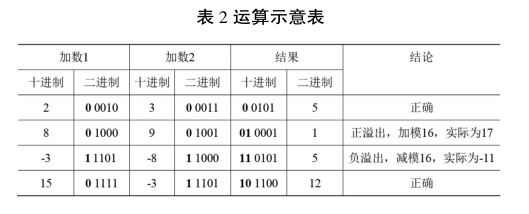
符号位有00，01，11，10四种可能，其中00，01代表正数；11，10代表负数；01为正溢出，10为负溢出。

分别以符号位为00，01，11，10四种举例说明，运算示意表如表2所示。

3实验仿真

使用十进制数进行一组加减，然后手动算法与设计算法进行比较。比如5+（-7），计算结果为-2，使用概念计算：

4结束语

讨论了原码、反码、补码的转化过程，简单介绍了如何使用程序来实现转换过程。具体说明了使用补码的运算过程，并且针对溢出问题进行了举例说明，并给出了根据溢出结果得到正确结果的方法。学习是一个不断积累的过程，在深入理解原码、反码和补码3种编码之间相互关系的同时，对计算机中数值的理解变得更加容易，能轻松地进行原码、反码、补码的相互转化，并且可以实现运算。

参考文献

[1]唐朔飞.计算机组成原理：第2版[M].北京：高等教育出版社， 2012.

[2]罗嘉庆，周世杰，徐洁.原码、反码和补码的教学探讨[J].计算机教育，2015（10）：42-45.

[3]孙丽.计算思维下再谈补码设计思想[J].电脑知识与技术， 2015，11（29）：70-71.

[4]听雨轩工作室.AgilentVEE虛拟仪器工程设计与开发[M].北京：国防工业出版社，2004.

[5]杨学颖，周建业.计算机补码概念探究[J].河南科技学院学报（自然科学版），2011，39（3）：90-94.

[6]哈马克.计算机组成与嵌入式系统：第6版[M].王国华，译.北京：机械工业出版社，2013.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。