《数学建模在警车调度问题中的应用》-理学论文，数学论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

数学建模在警车调度问题中的应用

范文

张岭

【摘要】警情对社会的影响程度，与警车到达警情点的时间有关，对警车的如何调度提出要求.本文通过构建警车调度数学模型，利用LINDO软件给出警车调度方案，使警情对社会的影响程度降到最低.

【关键词】警车调度;数学模型;LINDO

【基金项目】江苏警官学院青年教师科研项目，项目编号：2017SJYSQ05.

一、案例回顾

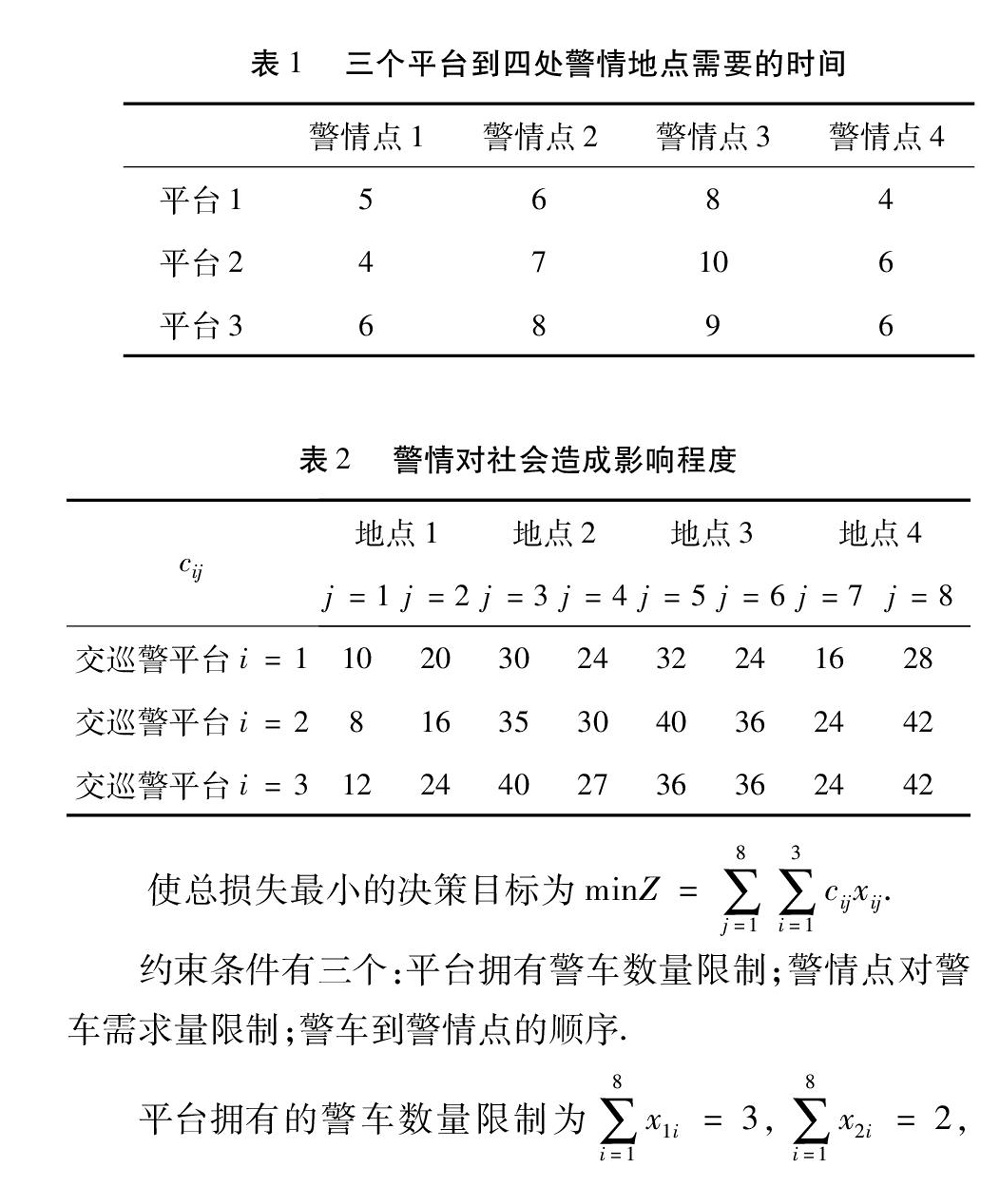
某地区同时接到四处警情，警情分別需要2辆、1辆、2辆和3辆警车，警情对社会的影响程度取决于警车到达及时程度，设tij为第j辆警车到达地点i的时间，警情对社会的影响程度为警车到达时间的线性函数，即2t11+4t12，5t21，3t31+4t32，6t41+4t42+7t43.可供调度的警车为8辆，属于三个交巡警平台（分别为3辆、2辆、3辆）.警车从三个平台到四个处警地点时间见表1.

二、模型建立及分析

分析：模型解决的主要问题是四处警情对社会的总损害程度最小，即四处警情的影响函数之和最小.用xij表示交巡警平台i是否向第j个需求点派车（1表示派车，0表示不派车）.计算出各警情点影响程度情况.

三、结论

从模型结果看，使警情点对社会影响程度总和最小化，分别从离该警情点用时最少的平台调度警车，可实现警情对社会影响程度的最小化.

【参考文献】

[1]谢金星，薛毅.优化建模与LINDO/LINGO软件[M].北京：清华大学出版社，2005：199-205.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。